Electing U.S. represenatives by coin flips would be 10,000 times better than our current system... literally
The target of this post is the seemingly minor quirks of using majority rules to elect congressional representatives. I think these quirks are at the root of processes which are putting an end to the democratic project in the US and UK. While, there are lots of overt issues which are tearing us apart (gun rights, abortion, etc.), our inability to have a civil discussion and iterate on an idea suggests the end is near for democracy. I use to blame the unhealthy state of democracy on partisanship and the gamification of politics, but I don’t anymore. I now blame partisanship and gamification on the rules of the game. In particular, I blame the majority rule.
There are a lot of alternative voting systems to majority rule. The most popular alternative is called ranked choice voting. However, my favorite one is lottery-voting and it goes like this:
- Select a random citizen (perhaps via a systematic use of coin flips).
- The selected citizen gets to cast a vote, which decideds the outcome of the election.
At face value this might look like a joke. It is not. Lottery voting grants the most voting power to the citizens of any other voting system one could devise. In this post we will quantify this voting power. The powerlessness you feel every election cycle is real because you do not have the power you are entitled to as a citizen.
What is wrong with majority rule
Imagine there are two candidates running for office labeled \(0\) and \(1\). Whichever candidate gets the majority of the votes wins in their district election.
- up to 50% of the population is ignored. If you live in a moderately populated area where 51% of people vote \(1\), then \(1\) wins the election in every single election. The 49% who vote for \(0\) are practically never represented.
- Safe districts. If you’ve secured 60% of the vote, and you’re in a disctrict of 10,000 people, then (under an IID model) the chance of you loosing the election is less than 1 in 10,000,000,000,000,000. I’d call this a safe district. Why bother voting! The representative of such a district could probably safely dabble in some minor nepotism.
- Conducting a fair election is hard and expensive. You need to think about accessibility for every single citizen. You need to secure school gyms, libraries, government buildings. You need an accurate census (which never happens). The census alone costs $15 billion. The cost of a election is difficult to calculate, but it’s also in the billions.
- Voter suppression This is the flip side of the last point. While it’s difficult to create a fair election, it’s not so difficult to make (systematically) unfair elections, and the people with power have every incentive to do so.
- Gerrymeandering. You can gain seats by consolidating all the opponent’s vote into one district, and spreading your parties votes to just barely break the 50% barier.
- Strategic voting. Given more than two options, (e.g. Democrats/Republicans/Liberatarians/Green), voters are incentivized to vote for the candidate with the most or second most support, anything else would be a waste of a vote. This is bad from a record keeping standpoint, because we don’t get good estimates of the true support of third party candidates. However, the real damage is the following.
- Emergent two-party oligarchy. The strategic voting aspect of majority rule yields a system where there are only two parties. This basically creates something like an oligarchy of political power.
- Nasty rhetoric. Under majority rule (or any system that aspires for high voter turnout) candidates are incentivized to rally a base, and generally discouraged from even speaking to those who are skeptical of their platform. The reasons for this are subtle, but will be expanded on later in the post.
I could go on whining, but I’ll cut myself short. There is a better system. It’s both better, and stupidererer. lottery voting (LV).1 Just a reminder, it works like this.
- Randomly select a citizen.
- The random citizen decides the election outcome.
There are some obvious flaws with system (non-deterministic for one), and I’ll address some of them later. For the moment just note that
- Nobody is ignored. A candidate with 10% of the vote will win 10% of the time.
- Parties are represented proportionately. At the level of congress the randomness tends to average out, and you will find that parties are represented proportionately to their support in the population. This is the same principle that states you will get approximately 50 heads and 50 tails if you flip an unbiased coin 100 times.
- No safe districts. If a politician “secures” 60% of the vote in a 10,000 member district, then her chance of loosing is 40%. She has to keep fighting because her opponent is not going to concede the election.
- Conducting an election is easy and cheap. Only one person needs to vote. If that person is serverly handicapped, has no arms or legs, that’s no problem, we can find a way.
- No voter suppression. There is only one voter, and nobody knows who it’s going to be. How can you suppress an electorate if you don’t know who they are?
- No Gerrymeandering. To call gerrymeandering under a lottery-vote “extremely difficult” would be an understatement. Exchanging votes between district A and B might increase your candidates likely-hood of winning distrit A by 2%, but it will neccessarily decrease your candidates chance of winning district B by the same 2% and will thus have net-zero impact on the make-up of the legislature.
- No strategic voting. There is literally no incentive to worry about other voters if you’re the voter chosen, because there are no other voters.
- More than two parties. Actually, this is kind of a problem too. You don’t get a two-party system (yay), but you do get an infinite party system (anybody who desires to run has a shot). Frankly, infinite parites is a major flaw for lottery voting, and I will provide a solution at the end. However, for the moment, assume that we have some mechanism in place to cap the number of candidates at something small like 2 or 3.
- Civil discussion across the aisle. Under a lottery vote it would be unwise for a candidate to bet that a base supporter is going to be selected on election day. In order to compete a candidate must be willing to convince skeptics of his platform or adjust his platform appropriately.
If I were to advertize lottery voting as a SAAS product, I’d probably have a table on the sales website that looked like this
| majority rule | lottery voting | |
|---|---|---|
| voter suppression | X | |
| gerrymeandering | X | |
| safe districts | X | |
| ignored voters | X | |
| tactical voting | X | |
| number of viable parties | 2 | \(\infty\) |
| nasty behavior | yes | no |
| random | no | yes |
| proportionate representation | no | yes |
| election cost | the economy of an island nation | $10.99 |
| voting power | \(10^{-15}\) | \(10^{-3}\) |
That last row of the table needs explanation, and we will devote the next section of the blog post to it. Voting power sounds like a “soft” concept, not a sharp quantitative one. However, it’s actually very quantifiable if you’re willing to endure some information theory.
A quantitative definition of voting power
Let \(\Omega\) be our event space and define the following random variables
| \(Y_{maj}: \Omega \to \{0,1\}\) | the outcome of the majority-rule based election |
| \(Y_{lot}: \Omega \to \{0,1\}\) | the outcome of the lotter-vote election |
| \(X:\Omega \to \{0,1\}\) | a particular vote |
We’d like to have some measure of how much the vote, \(X\), influences the election outcomes, \(Y_{maj}\) and \(Y_{lot}\).
The canonical measure of the influence one random variable exerts upon another is mutual information:
\[MI(X,Y) = \sum_{x=0,y=0}^{1,1} \Pr(X=x, Y=y) \log \left( \frac{\Pr(X=x,Y=y) }{\Pr(X=x) \Pr(Y=y)} \right)\]So it’s natural for us to define the voting power of a voter in a majority rule system as \(MI(X, Y_{maj})\), and similarly for a lottery vote we’d seek to measure \(MI(X, Y_{lot})\).
The concept of mutual information was invented by Claude Shannon in the 1940s at Bell Laboratories as a measure of how faithfully information through a noisy channel. While that might sound irrelevent, it is not. The relationship between your vote and the outcome of the election is that of a sender communicating to a reciever through a noisy channel. The degree to which the make-up of the country reflects our beliefs requires that this channel have a high mutual information for each citizen.
Computing mutual information
In order to calculate mutual information, we need to specify the joint probabilities \(\Pr(X, Y_{maj})\) and \(\Pr(X, Y_{lot})\). Let’s start by modeling the voters. In an ideal world everybody is an independent thinker and therefore contributes useful information, which is not duplicated by any other voter when they cast their vote. As the inner workings of each voter are unkown to us, this intellectual independence manifests as statistical independence. Mathematically, this means that each voter’s vote is modeled is an independent (biased) coin flip with some bias \(\theta \in [0,1]\). As \(X\) denotes an arbitrary vote, we have that
\[\Pr(X=0) = \theta\]and if we define \(N_0: \Omega \to \mathbb{N}\) as the number of votes cast to candidate \(0\), then, \(N_0\) is binomially distributed, as it’s merely the sum of iid coin flips. That is to say, given a population of size \(n\) we know
\[\Pr(N_0 = k) = \binom{n}{k} \theta^k (1-\theta)^{n-k}\]On first glance this is a really dumb model. Assuming all voters think independently of one another is naive at best. However, this post is a critique of majority rule democracy. Such a system works best when all the voters are independent thinkers. We should only expect the performance of a majority rule system to degrade as voters become less independent. In this sense, this coin-flip voter model is ideal for the aims of this blog post as it presents the best-case scenario for a majority rule system.
The other advantage of this model is it’s computable with pen and paper. In particular, we can compute the probability the event \(N_0 \geq n / 2\), which is the event whereing candidate \(0\) wins the election under a majoritarian system. In fact we can compute the full joint probability \(\Pr(Y_{maj},X)\)
\[\begin{align} \Pr(Y_{maj}=0, X=0) &= F( \lfloor n/2 \rfloor-1, n-1, 1-\theta) \theta \\ \Pr(Y_{maj}=1, X=1) &= F(\lfloor n/2 \rfloor -1, n-1, \theta) \cdot (1-\theta) \\ \Pr(Y_{maj}=0, X=1) &= F(\lceil n/2 \rceil; n-1,\theta) \cdot (1-\theta) \\ \Pr(Y_{maj}=1, X=0) &= F(\lceil n/2 \rceil; n-1, 1-\theta) \cdot \theta \end{align}\]Where \(F(m,n,p) = \sum_{k < m} \binom{n}{k} p^k (1-p)^{n-k}\) is the cumulative mass function of the binomial distribution.
(Click here for derivation)
First note that $$ Y_{maj} = 0 \iff N_0 > n/2 $$ We know that N_0 is binomially distributed and so we can compute $$ \begin{align} \Pr(Y_{maj}=0, X=0) &= \Pr(N_0 > n/2, X=0) \\ &= \Pr(N_0 > n/2 | X=0) \Pr(X=0) \\ &= \Pr(N_1 < n/2 | X=0) \theta \\ &= F( \lfloor n/2 \rfloor-1, n-1, 1-\theta) \theta \end{align} $$ Noting that $$\Pr(Y_{maj}=1 \mid X=0) = 1 - \Pr(Y_{maj}=0 \mid X=0)$$ and invoking a "0<->1" symmetry we can derive the remaining 3 probabilities. QED.Similarly, we can compute the joint probability \(\Pr(Y_{lot}, X)\)
\[\begin{align} \Pr(X=1, Y_{lot}=0) &= \theta \frac{n-1}{n} \\ \Pr(X=0, Y_{lot}=1) &= (1-\theta) \frac{n-1}{n} \\ \Pr(X=0, Y_{lot}=0) &= \left( \frac{1}{n} + \theta \frac{n-1}{n} \right) \theta \\ \Pr(X=1, Y_{lot}=1) &= \left( \frac{1}{n} + (1-\theta) \frac{n-1}{n} \right) (1-\theta) \end{align}\](Click for derivation)
Let $$Z:\Omega \to \{True,False\}$$ be the boolean valued random variable which is true if the voter in question is chosen in the lottery vote. You can then use the law of total probability to compute all the relevent quantities. For example, we can compute $$ \begin{align} \Pr(X=0, Y_{lot}=0) &= \Pr(Y_{lot}=0 | X=0) \Pr(X=0) \\ &= \left( \sum_{z \in \{T,F\}} \Pr( Y_{lot}, Z=z | X=0)\right)\theta \\ &= \left( \sum_{z \in \{T,F\}} \Pr(Y_{lot}| Z=z, X=0) \Pr(Z=z) \right) \theta \\ &= \left( \frac{1}{n} + \theta \frac{n-1}{n} \right) \theta \end{align} $$ We can compute the remaining three probabilities similarly, or we may invoke the law of total probability and the "0<->1" symmtry to ge them. QED.Now that we have the full joint probabilitiy distributions for \(\Pr(X,Y_{maj})\) and \(\Pr(X,Y_{lot})\) we can compute the mutual information \(MI(X,Y_{maj})\) and \(MI(X, Y_{lot})\). In partcular, we can see how voting power scales with the population size, \(n\). One would expect the voting power of an individual citizen to decay as the population goes up. The question is, how fast is the decay?
We will find later that majority rule decays slower when \(\theta\) is close to 0.5. If you use the outcome of the 2022 election to estimate \(\theta\) you’d come to the conclusion that such a scenario is unlikely. For example you’d find the median estimate is \(\hat{\theta} = 0.23\)2. Moreover, you’d find 98% of districts have an estimated \(\hat{\theta}\) which is less than 0.45. So to be generous to the case of majority-rule base voting, lets consider the case where \(\theta = 0.45\) to see how things play out.
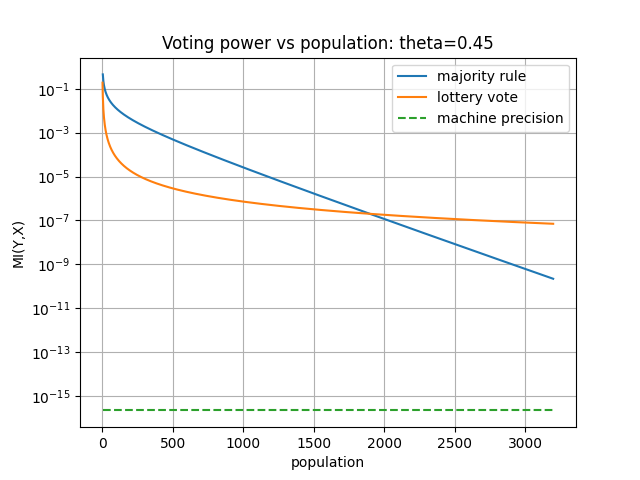
Note that the median population size in a given district is 535,0003. I can not even create a plot for such a population because I will get an underflow error (see the machine precision in the above plot). However, one can see from the plot that voting power under a majority-rule based election decays exponentially. When we get to populations in the 100,000s range we find that majority rule is literally 100,000 times worse than lottery voting. Just to re-iterate, this is the best scenario for majority rule. In most voting districts majority rule decays much faster and these curve cross much earlier.
For small populations both of these systems are comparable, and many people might feel that majority rule is better at the small scale. Our lived experiance is in a world where groups of people are in the dozens, and we probably only have a couple hundred names in our phones. With a lived experiance like this it’s easy to grow comfortable with majority rule. However, this intuition apparently does not scale to the size of a voting district. Much like how our daily experience with physics at the human scale does not transfer to a good intuition at the cosmic/quantum scale, I would argue our intuition for elections at the human scale (n<50) does not transfer to elections at the electoral district scale (n>10,000).
Rigorous derivation of scaling laws
One can see from the logarithmic plot earlier that voting power for majority-rule systems decays exponentailly with population size \(n\). In fact, we don’t need to settle for plots. We can rigorously prove the upper bound
\[MI(Y_{maj}, X) \leq e^{ - D\left(\frac{1}{2} \| \theta\right) (n-1)}\]where \(D(\frac{1}{2} \| \theta)\) is the KL-divergence between a coin of bias \(\theta\) and a fair coin.
(to see proof click here)
We can write $$ MI(Y_{maj}, X) = \sum_{x=0,y=0}^{1,2} T_{xy} $$ where $$ T_{xy} := \Pr(X=x, Y_{maj}=y) \left( \log( \Pr(Y_{maj}=y|X=x) ) - \log(\Pr(Y_{maj}=y) ) \right) $$ Voting for candidate 1 reduces the likelyhood that candidate 0 will win and vise-versa. Thus $$ \Pr(Y_{maj}=0 | X=1) < \Pr(Y=0) \quad \text{and} \quad \Pr(Y_{maj}=1 | X=0) < \Pr(Y_{maj}=1). $$ This implies that $$ T_{01} < 0 \quad \text{and} \quad T_{10} < 0. $$ Therefore $$MI(Y_{maj}, X) < T_{00} + T_{11}.$$ Lets focus on the first term. $$ T_{00} = \Pr(Y_{mr}=0, X=0) \left( \log(\Pr(Y_{mr}=0 | X=0) ) - \log(\Pr(Y_{mr}=0)) \right) $$ Since `log` is a concave function, it's bounded by a linear approximation. We can use the derivative at $$z=Pr(Y_{maj}=0 \mid X=0)$$ to find that $$ T_{00} \leq \frac{\Pr(Y_{maj}=0,X=0)}{\Pr(Y_{maj}=0| X=0)} \left( \Pr(Y_{maj}=0|X=0) - \Pr(Y_{maj}=0) \right) $$ noting that $$\Pr(X=0)=\theta$$ and invoking Baye's theorem gives $$ T_{00} \leq \theta \left( \Pr(Y_{maj}=0|X=0) - \Pr(Y_{maj}=0) \right) $$ Let's denote the cdf for the binomial distribution by $$F(k; n, p)$$ where $$p$$ is the bias of the coin flips. We can equate $$ \Pr(Y_{maj}=0) = \Pr(N_1 < n/2) = F\left(\left\lfloor\frac{n}{2}\right\rfloor ; n , \phi\right) $$ and $$ \Pr(Y_{maj}=0|X=0) = \Pr(N_1 < n/2 | X=0) = F\left(\left\lfloor\frac{n}{2}\right\rfloor-1 ; n-1 , \phi\right) $$ Now is the time to fire-up-the-google for help. On the wikipedia page for the binomial distribution they include some useful bounds. Wlog, assume $$\theta < 1/2$$. The claim is that $$ \left( 8n \frac{k}{n}\left(1-\frac{k}{n}\right)\right)^{-1/2} e^{-D(k/n||\phi) n} \leq F(k;n,\phi) \leq e^{-D(k/n||phi) n} $$ where $$ D(a \| p) := a \log \left( \frac{a}{p} \right) + \left( 1- a \right) \log \left( \frac{1-a}{1-p} \right)$$ We see that $$ \Pr(Y_{maj}=0) \geq \left(2n\right)^{-1/2} \exp(-nD(\lfloor n/2 \rfloor / n ||\phi)) $$ and $$ \Pr(Y_{maj}=0|X=0) \leq \exp( - (n-1) D\left( \frac{\lfloor n/2 \rfloor-1}{n-1} || \phi) \right) $$ To make typesetting easier, lets define $$m := \lfloor n/2 \rfloor$$. Inserting the above equation into the previous inequality we have the bound $$ T_{00} \leq \theta \left( \exp\left( - (n-1) D\left( \frac{m-1}{n-1} || \phi\right) \right) - \left(2n\right)^{-1/2} \exp(-nD(m/n||\phi)) \right) $$ This is algebraically quite annoying, and we can loosen the bound to get something easier on the eyes $$ T_{00} \leq \theta \exp(- (n-1) \kappa_\phi) $$ where $$\kappa_\phi = \min( D(\frac{m}{n} \| \phi), D(\frac{m-1}{n-1} \| \phi) )$$ Doing the same excercise for $$T_{11}$$ (or by using symmetries) yields the bound $$T_{11} \leq \phi \exp( - (n-1) \kappa_\theta)$$. So we have the total bound $$ MI(Y_{maj}, X) \leq \theta \exp( - (n-1) \kappa_\phi) + \phi \exp( - (n-1) \kappa_\theta) $$ which we can simplify further to $$ MI(Y_{maj}, X) \leq \exp( - \kappa (n-1)) $$ where $$\kappa = \min(\kappa_\phi, \kappa_\theta)$$. Note that for large $$n$$ we have that $$\kappa \approx D( 1/2 \| \phi)$$. QED.In contrast, for lottery voting we have the scaling law
\[MI(Y_{lot}, X) \sim n^{-2}\]which is “proven” by simply observing the formula for \(MI(Y_{lot}, X)\) and taking the leading order term in \(n\).
Variable \(\theta\) and campaign strategy
So far we’ve assumed a homogenous population, where everybody is tagged with the same value for \(\theta\). However, from the perspective of a campaign strategist, it’s typically the case that \(\theta\) is estimated as a function of known things. For example a campaign strategist might cross reference polls with demographic data to estimate a different \(\theta\) for each district and ethnicity. So you’d have a different \(\theta\) for each voter profile, i.e. one for “affluent asians” with zip code 43093, and another for low income white people with zip code 43083.
As we saw in the previous section, under majority rule, voting power decays exponentially quickly at a rate of \(D(\theta \| 0.5)\). If there are two demographics, with estimated \(\theta\)’s of value \(\theta_1\) and \(\theta_2\), then the ratio of one demographics voting power vs anothers is \(MI(X_1, Y_{maj}) / MI(X_2, Y_{maj}) \sim \exp( - n D(\theta_1 \| \theta_2))\). In words this means not all voters are equal and voting power diverges exponentially with population size. In particular, the voters with the most power are ones where \(\theta \approx 0.5\), these are the swing voters. No surprise the swing states get all the attention.4 This article from nationalpopularvote.com captures the inequality quite clearly
Seven out of eight dollars for TV ads up to mid-October ($884,000,000 of $1,015,000,000) were spent in the same 6 states (Florida, Michigan, Pennsylvania, Wisconsin, Virginia, and Ardzona).
All of those states were swing states in the 2020 election. Another quote to drive the point home
The reason why voters in only a handful of states matter in presidential races is that almost all states award all of their electoral votes to the candidate who gets the most votes inside the state. Because of these state winner-take-all laws, candidates have no reason to pay attention to voters unless they live in a state where the race is within a few percentage points.
This sort of bias can be fixed (in the case of congressional elections) by switching to a proportional representation voting system. Any proportional representation system would be an improvement, lottery voting being only one such manifestation. However, lottery voting has the virtue of immunity from the problems associated with demanding voter turnout.
Problems with demanding voter turnout?
Yes, demanding voter turnout is a problem. It might sound counter intuitive because higher voter turnout leads to better election outcomes under our current system. In fact, most proposed voting systems (e.g. ranked choice voting) also perform better with high voter turnout. Lottery voting is the only system I know of that turns this on its head. Roughly speaking there are two issues with electoral systems that aspire for maximal voter turnout
- The election results are biased if voter turnout is low and biased
- Campaigns are incentivized to maximize turnout of supporters as opposed to improving/explaining their platform
The second point is rather subtle, and we will come back to it. The first point is intuitive enough, and is almost captured by our model. We can complexify our model a bit by adding an intermediate variable for each voter, which is the probability that they will actually show up to the ballot box. I won’t go into the details, but at a high level the number of people who vote is a binomially distributed random variable, and the results of the previous sections have a bit of bell-curve shaped noise around them. This does not really change any of the conclusions of the previous sections. However, there is one new source of bias which is a bias caused by biased voter turnout. If people who vote for candidate \(0\) are less (or more) likely to turnout than voter turnout obviously biases the election result. For large populations, this bias becomes very easy to predict (the uncertainty decreases like \(1/\sqrt{n}\)). Under majority rule, the best strategy is to rally people who are already on your side to vote.
Encouraging people to vote sounds like a good thing. If both sides manage to get every single citizen to vote, the bias dissapears. However, in practice we get voter turnout in the ball-park of 40-60\% for federal elections. In this range, the bias towards one candidate is measurable, and it’s the reason for all the hoopla about voter IDs and election security.
This bias is a bad thing, but the real harm is that we have candidates focusing on voter turnout in order to leverage the bias in their favor. Under majority rule, the optimal campaign strategy is to rally people who already agree with your platform. Reaching across the aisle is for dumdums. I don’t think it’s an exaggeration to argue that our us-vs-them mentality in the US is the result of two ingredients
- The use of majority rule, which puts virtually all the voting power in swing districts
- The expectation that everybody vote (even though this never happens), which forced campaigns to compete on voter turnout as opposed to the power of their ideas
In contrast, lottery voting does not have swing districts, and since only one (random) person votes, there is no incentive for candidates to appeal to a base. In fact, it’s almost the opposite situation. Under a lottery vote, the optimal strategy is to target people who are not fully on board with your platform. There is some fancy schmancy theory for this, but the basic reason is intuitive enough. If you rally people who are already going to vote for you (assuming they are picked to vote in the lottery) then you have accomplished nothing because on election day only one vote is going to decide the winner, and those base supporters were going to vote for you anyway. Therefore, the only strategy is to widen your base. In particular, if you actually change the mind of a skeptic, then you actually do improve your odds of winning the election. Candidates who simply shout into the echo-chamber of pre-existing supporters are not competitive under a lottery vote. As a result, lottery voting could have profound effects on the tone of our politics.
Admittedly, even in majority rule it is true that candidates are incentivized to widen their base. The issue is that in majority rule there are two strategies: widen base or rally voter turnout of existing base. It’s not obvious apriori which strategy is the most rewarding, and candidates do a mix of both typically. However, every election in my lifetime has put a lot of emphasis on the voter-turnout strategy, and this is not in our collective interest.
Optimal (obnoxious) campaigning
Let me reiterate the last couple sections in the language of optimization and games. When you are faced with a game, and asked to come up with a strategy, you must consider every means at your disposal if you want to win. The more levers and variables to pull, the more solutions you’ll need to consider. On the flip side, from the perspective of the game designer, more levers and variables makes it harder to predict the behavior of the players. There could be some unintended strategies. I think elections that aspire for high voter turnout are creating a game with some strategies that were not intended by the founders (at least the cool ones).
In the case of lottery voting, the election is so stupidly simple that there is not a lot of things a candidate can do except for advocate his platform to convert people to his side, or alter his platform to satisfy more voters (both are good). To me this sounds like a conversation between the candidates and the citizenry about the direction of the country, and this conversation takes input from all people equally.
I think the founding father’s probably intended to design a system where candidates had a back-and-forth with the populous. Unfortunately, in creating a system that aspires for maximal voter turnout added extra variables which a campaign strategist can use, and which are acted upon independently of how convincing a candidate platform may be. Yes, the candidate can advocate for his platform and try to convert people to his side, but it would be stupid too exert much energy there. A saavy campaign strategist will work to optimize voter turnout among voter profiles that already support the candidate. This is an issue with any voting system that assumes high voter turnout (this includes ranked choice voting). Moreover, in the case of majority-rule we get the notion of a swing districts, which have the most voting power. This is the origin of obnoxious campaign rallies in Florida and Pennsylvania.
Critiques of Lottery Voting
There’s not a lot of literature on lottery voting out there. Since nobody is currently actively advocating for it, there is also not a lot of criticism. I’ll list a few that I predict reasonable people might have.
Critique 1: We might live under minority rule
If we apply the lottery vote system to a presendential election, then “yes” this is a possibility. Perhaps electing the chief executive by some rando is a bad idea.5 However, when applied to congress, the worry of minority rule is not well founded. If 60% of the population supports one of the major parties, then that party will mostly likely get 60% of the seats. Yes, some districts will be assigned representatives from the minority party (e.g. a majority “0” district will get a 1), but the errors go both ways so that (by the central limit theorem) in aggregate you will get a congress that represents the nation proportionately. It’s the same logic that tells us that if you flip a six-sided die 120 times then about 20 of the rolls should be sixes. The minor random noise of a lottery vote is possibly smaller than the biases introduced in elections where we expect everybody to vote yet only observe 50% voter turnout. Being approximately correct with bounded randomness is better than being exactly incorrect with high certainty. This is, more or less, one of the arguments in favor of lottery voting put forth by law professor, Akhil Reed Amar, in a 1984 article of the Yale Law Journal..
Critique 2: Too many candidates
This is the critique that troubles me the most, and frankly it’s so serious that I would concede that naive lottery voting is a bad idea. Under a lottery vote there is almost no incentive not to run for office. Anybody with a modicum of political ambitions will run. This seems bad for numerous reasons. For one, the populous could not possibly evaluate this many people. Moreover, all the analysis I’ve done so far assumes the number of candidates is small. It doesn’t break if there are only 2-5 candidates, but it does break eventually. Lastly, having tons of wasteful elections is a hidden cost that eats away at all the savings from doing a lottery vote.
One solution to this issue is to have two rounds in the election. In the first round we randomly sample a relatively small number, \(N\), of citizens (\(N < 1000\)). Those citizens then do a deterministic election (perhaps plurality based, perhaps ranked choice). The top \(k\) candidates proceed to the final round, which is the then decided by a lottery vote. As long as \(N\) is small this is still cheap. Here, \(k\) could be something small like 2 or 3. Note that if \(k=1\) and we use plurality, then we are effectively going to end up in a majority rule system (the emergent state is two competitive parties). So \(k\) can be seen as a parameter which interpolates between majority rule (\(k=1\)) and a true lottery vote (\(k=\infty\)). In particular, using a rational actor model of the citizens, we should expect \(k+1\) major political parties under this two-step voting process.
I’ll admit this is a bandaid solution and I’m sure there are better fixes. What I like about this fix is that it does not incentivize voter-turnout-centric campaigning because it only demands a small number of voters come to the polls.
Critique 3: More campaign ads?!
Yeah, more candidates, with more competitive races probably means more campaign ads. As discussed, I do think that lottery voting has the potential to change the political game in a way that will make the ads less nasty, but… yeah, quite possibly more campaign ads.
Critique 4: What about [ALTERNATIVE VOTING SYSTEM]?
There are a lot of decent alternatives to majority rule (or plurality based) elections. Ranked choice voting seems to be the favored system by people who are taking real action to change our elections. More power to them! I hope they succeed. However, in the context of electing congressiona l representatives I do think lottery voting is strictly better
- it’s cheap
- it’s impossible to gamify (because it’s so stupid simple)
- because it’s impossible to gamify, candidates are forced to appeal to all voters
- it’s proportionate
No other alternative voting system competes with lottery voting on all these points. The stochasticity of lottery voting is scary, but in the context of electing congress it’s a good thing because you elect hundreds of representatives and all that randomness gets averaged into a congress which represents our views accurately (in all their contradictory glory). It’s the same principle that says if you flip a coin 1000 times, you’ll get approximately 500 heads.
Just to re-iterate, all egalitarian deterministic voting systems (like party-list proportionate representation for example) request every single citizen vote. This request introduces a major bias when there is less than stellar voter turnout because there are correllations between voter preferences and voter turnout. Therefore, a deterministic voter system that is proportionate in theory, is not really proportionate in practice. Moreover, the game-theory of campaigning under a system that requests full voter turnout is nasty and quite possibly is the cause of a good deal of uncivil demonization of compromise (and ultimately progress) among our politicians. In contrast, the lottery vote only requires a single vote, and we can drive any bias down to near zero. I have no faith we can make voting accessible for all citizens without bias, but I do have faith we can do it for a single random citizen.
Critique 5: This will never happen
Well…. yeah. However, one can dream. The big obstacles are
- Nobody knows how awesome lottery voting is
- People who are currently elected have little incentive to makes such a change
The first bullet is easily addressed by sharing this blog-post and doing all the normal internet stuff (twitter/facebook/i/hate/the/internet/instagram/snapchat). The second bullet point requires more ingenuity. I think there is a massive prisoners dillemma that we’d need to break out of. There are ways of perturbing the shitty Nash equilibrium of the prisoner’s dillemma. If I manage to flesh this out I will jot it down, but frankly I’m stumped.
That said, who gives a damn! If we only talk about things that are probably going to happen, then why bother talking at all?
Closing remarks
I think it’s a shame that we view half of the nation as enemies rather than fellow citizens. The only realistic way to win elections under our current system is to rehash old ideas to galvanize base voters while secretly working to suppress those of the opponent. Candidates are not incentivized to bring new ideas to the table or neccessarily solve any issues. Moreover, our system deprives voters of most of their voting power and then distributes the little that remains very uneuqally. In fact I do not really like any voting system that aspires for full voter turnout now because the rules of the game make candidates nastier as they get smarter at playing it. The quirks mentioned are very corrosive, and over the course of decades I think these quirks have resulted in an electorate that feels powerless (because they are), and candidates who are often very nasty people. Lottery voting might not be a silver bullet but it could play a big role in solving this mess. Please share the good news.
Shoutouts
- Special thanks to my dad for pointint out the wikipedia article on lottery voting.
- Shoutout to Mr. Wohl for clearing up some pretty big oversites.
- Shoutout to La Burrita which supplies the burritoes required to support his research.
Footnotes
-
See the wikipedia article ↩
-
This is a maximum liklihood estimate obtained from this dataset. ↩
-
According to 2018 census data) ↩
-
The swing states are where 99% of campaign ad revenue and time is spent, https://www.nytimes.com/interactive/2020/10/17/us/politics/trump-biden-campaign-ad-spending.html ↩
-
It might be a good idea to elect the presedent using a lottery vote. I’m really not sure. It’s not really covered in this blog post. ↩